在进行 Cox 比例风险回归后，可能需要研究模型在描述输入数据方面的表现。评估这种拟合优度的一种方法是比较模型估计的每个个体的危险度和输入数据中观察到的这些相同个体的生存时间。

简短版本

Prism 报告 Harrell 的 C（一致性）统计量值及其相关的 95% 置信区间。要计算 C 统计量，需要考虑所有可能的观测对，其中至少有一个观测对包含一个事件（计算中省略了两个观测对都被删剪的情况）。对每对观测值，比较观测时间（"T"，输入表格）和相对风险（"XB"，由模型确定）。如果事件发生时间较短的观测值同时也是相对风险较高的观测值，则这对观测值被认为是 "一致的"（这些观测值对中，模型通过赋予较高的相对风险，正确识别了生存时间较短的观测值）。不拟合这种期望值关系的观测对被视为 "不一致"（或者在某些情况下，根本无法被识别为 "一致"，因为它们的观察时间或相对风险评分的成对值都是并列的，见下文 "详细版本"）。

 

C 统计量表示一致配对的比例（模型正确预测生存时间较短的配对所占的比例），因此其值介于 0 和 1 之间。因此，C 统计量接近 1 的模型表明该模型具有较好的判别能力，而 C 统计量接近 0.5 的模型并不比随机概率好。C 统计量小于 0.5 的模型极为罕见，一般只会出现在样本量非常小的情况下。如果 C 统计量小于 0.5，那么很可能是出了什么问题！

C 统计量背后的直觉

对于给定的观察值，相对风险 (XB) 值越大，表明危险性越高，因此存活时间越短。因此，如果一个观察值比另一个观察值具有更高的 XB 值和更短的事件发生时间，则可以认为这些观察值的表现符合期望值。但是，如果一个观察值比另一个观察值的 XB 值更高，而到相关事件的经过时间更长，则可以认为这些观察值的表现异常。一致性简单来说就是行为符合期望值的数据对的比例（假设任何观察值对之间的相对风险值没有联系）。

解读一致性的另一种方法是将模型视为一种预测工具。当出现两个观测数据时，该模型将预测这两个观测数据中哪一个的存活时间更长。一个完美的预测设备会正确预测每一对观察结果，而一个真正随机的设备预计只能正确预测一半的观察结果（把模型想象成一个掷硬币决定哪个观察结果具有更高的相对风险的设备：我们预计它大约有 50% 的时间是正确的）。

一致性值反映了这种行为，其值必须介于 0 和 1 之间。成对值为 1 意味着模型正确预测了所有观察值对（预测寿命更长的观察值确实寿命更长，预测更早经历相关事件的观察值确实更早经历）。如果模型确实是随机的，那么这个一致性值将为 0.5，表明有一半的时间，模型会正确预测哪个观察值 "存活 "的时间更长，直到感兴趣的事件发生。

如果这个拟合优度的概念听起来类似于逻辑回归所报告的 ROC 曲线下面积的拟合优度指标，那是因为这两个概念是绝对等同的。

详细版本

回顾一下 Cox 比例风险的模型：

 

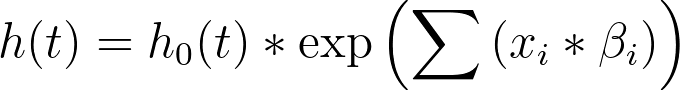
可以重新排列为以下形式：

 

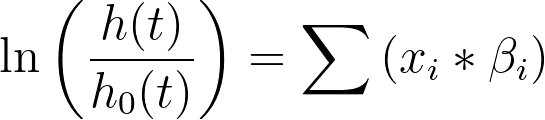
请注意，在 Cox 回归中，"xi"表示预测因子变量（如年龄、体重、治疗组等）的值。

Cox 比例风险实际上并没有为基线风险假设任何特异性的形式，但可以看出，线性预测因子（Σxi*βi，简称 "XB"）与风险率（h(t)）成正比。这意味着随着 XB 值的增加，危险率也会增加。随后，随着危险率的增加，发生相关事件的概率也会增加，因此预计存活时间会缩短。

总之，XB 越大，预测发生相关事件的时间越短。

利用计算出的参数系数（β）和输入数据表中观察到的事件发生时间数据，我们可以评估模型在预测这种关系方面的性能如何。这可以通过哈雷尔 C 统计量来实现。

该值由弗兰克-哈雷尔（Frank Harrell）(1) 推广，可作如下解读：

•考虑输入数据表中至少有一个观测值是事件的每一个可能的观测值配对组合（两个观测值都被删剪的配对在计算中省略）。

如果观测对中的两个观测值都包含一个事件

•将模型确定的线性预测因子 (XB) 和观测时间与输入数据中每个观测值的相关事件进行比较

▪为便于记述，我们将第一个观测值的相对风险称为XB1，第二个观测值的相对风险称为XB2，第一个观测值的经过时间称为T1，第二个观测值的经过时间称为T2。

•如果出现以下情况，则认为观察结果对 "一致"：

▪XB1>XB2且T1<T2

▪XB2<XB2且T1>T2

•如果出现以下情况，则认为这对观测值 "不一致"：

▪XB1>XB2且T1>T2

▪XB1<XB2且T1<T2

•如果出现以下情况，则观测对被视为 "XB 并列"：

▪XB1=XB2

•在下列情况下，观测对被视为 "T 平分"： XB1 = XB2

▪T1=T2

•在下列情况下，观测对被视为 "在 XB 和 T 中并列"：

▪XB1=XB2且T1=T2

如果观测对中有一个观测值被删剪

•在以下定义中，发生事件的观测值的观测时间为Te，相对风险为XBe，而被删剪的观测值的观测时间为Tc，相对风险为XBc

•如果Tc<Te，那么我们就无法确定谁先经历了事件（被删剪观测值的个体在事件发生前离开），因此这对观测值在计算中被省略了

•如果出现以下情况，这对观测值将被视为 "一致"：

▪Tc≥Te且XBc<XBe

•如果出现以下情况，则这对观测值被视为 "不一致"：

▪Tc≥Te且XBc>XBe

•如果出现以下情况，则这对观测值被视为 "XB 并列"：

▪XBc=XBe

•有一个删剪和一个事件的观测值对不能在 T 中并列

 

一致统计量公式

利用上述定义，确定以下内容：

•nconcordant，一致的观测对数

•ndiscordant，不一致的事件对数

•ntiedin XB，XB 中并列的线对数

当 XB 中任何一对观测值都不存在并列关系时，C 统计量的计算公式如下：

 

 

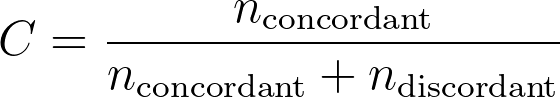
这表示模型能够正确分配适当相对风险值的观察值的"分数"（相对风险值越高，存活时间越短）。如果在所有观测对中，相对风险值较大的观测对同时也是存活时间较短的观测对，那么所有观测对都是一致的，这个分数就等于 1！当有成对观察值的相对风险值相同时，计算公式略有不同：

 

 

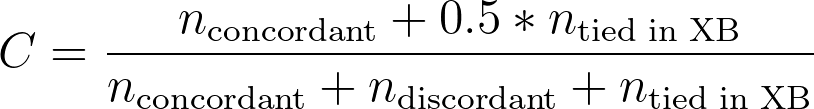
这个公式与之类似，但在分子和分母中都增加了一个表示并列观测值的项。回到前一节的"预测因子"本示例，我们可以考虑当模型中出现线性预测因子（XB）并列的观测值时，会发生什么情况。在这种情况下，预测装置无法知道哪个观测值应该存活更长时间，因此它只能通过掷硬币来做出决定。我们预计掷硬币的正确率约为 50%，这就是为什么在上述等式的分子中，XB 中并列的观测对数要乘以 0.5。因此，在这种情况下，C 统计量仍然代表模型能够正确分配适当相对风险值的观察值的比例。

参考文献

1.Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA.评估医学检验的收益率。美国医学会杂志》。1982;247:2543-46.