Prism 提供四种正态性检验方法。为什么检验正态性的方法不止一种？答案与所有正态性检验的对象有关：评估值是否来自正态分布。一个分布偏离正态性的方式有无数种，因此需要有各种不同类型的正态性检验也就在情理之中了。每种不同的正态性检验都会在数据中寻找不同的东西，因此每种检验都会给出不同的结果。

D'Agostino-Pearson：用形状评估正态性

D'Agostino-Pearson正态性检验首先计算偏斜度和峰度，以量化分布在不对称和形状方面离高斯分布有多远。然后，计算这两个值与高斯分布期望值的差异程度，并根据这些差异的总和计算出一个 P 值。这是一种通用且功能强大的正态性检验，一般推荐使用。但需要注意的是，这一建议也有例外。特异性是，当一个分布的偏斜度和峰度非常接近正态分布，但绝对是非正态分布时，该检验将无法确定该分布为非正态分布。下面的分布就是本示例。

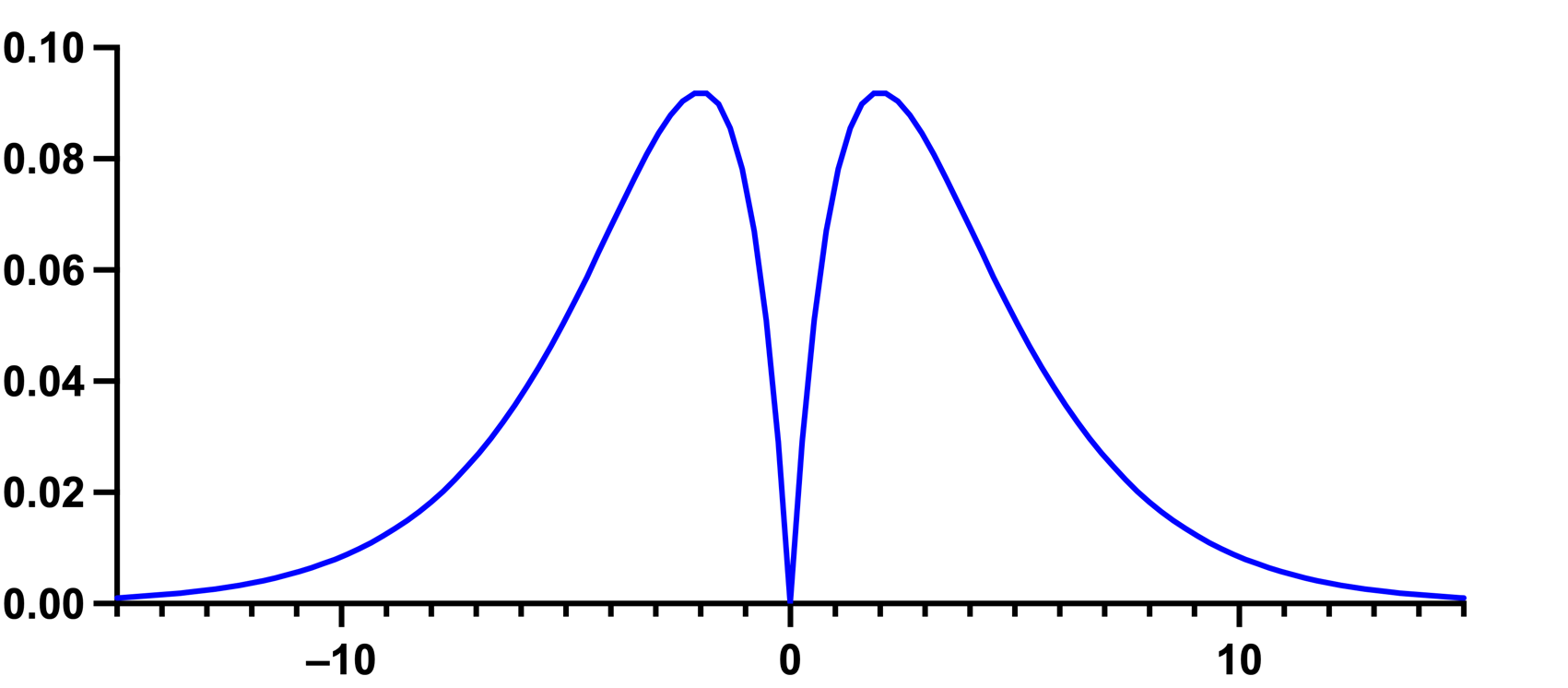
该分布的偏斜度为 0，峰度为 3.0（过度峰度为 0）：与正态分布的值完全相同。因此，D'Agostino-Pearson 检验无法将此分布识别为非正态性分布（尽管它显然是）。请注意，达戈斯蒂诺开发了多种正态性检验方法。Prism 使用的是 "omnibus K2 "检验。

Shapiro-Wilk：用标准偏差评估正态性

说到正态性检验，Shapiro-Wilk 检验是另一种流行的选择。与D'Agostino-Pearson检验不同，Shapiro-Wilk检验不使用分布的形状来判断是否正态性。相反，它将数据的实际 SD 与根据数据 QQ 图斜率计算出的 SD 进行比较，并计算出两者的比值。如果数据是从高斯分布中采样的，那么这两个值将是相似的，因此比值将接近 1.0，而比值与 1 相差很大，则表明数据是非正态分布。如果每个值都是唯一的，Shapiro-Wilk 检验的效果就会非常好，但如果有几个值是相同的，效果就会差一些。Shapiro-Wilk检验有多种计算方法。Prism 使用 Royston (1) 方法。Prism 只能在样本量小于 5000 时计算 Shapiro-Wilk 检验。

Anderson-Darling 检验和 Kolmogorov-Smirnov 检验：用累积分布评估正态性

Anderson-Darling 检验和 Kolmogorov-Smirnov 检验都使用累积分布来确定数据是否从正态分布中采样。这两种检验都将实际累积分布与正态性分布的理想累积分布进行比较。不过，两种检验的比较方式不同。

Anderson-Darling检验通过比较数据集的累积分布和高斯分布的理想累积分布来计算P值。它考虑了累积分布曲线各部分的差异。

与 Anderson-Darling 检验不同的是，Kolmogorov-Smirnov 检验通过单一值计算 P 值：数据的累积分布与高斯分布累积值之间的最大差异。这不是一种非常灵敏的评估正态性的方法，我们现在同意这样的说法："Kolmogorov-Smirnov 检验只是一种历史奇观。它不应该被使用"(2)。Kolmogorov-Smirnov 检验是 Prism 早期版本提供的唯一检验方法。我们仍然提供这种检验（为了保持一致性），但不再推荐使用。如果我们不再推荐使用该检验，为什么还包含它呢？最初，该检验是 Prism 提供的唯一正态性检验。我们现在包含它只是为了与旧版本软件生成的文件和结果保持一致。我们不建议使用 Kolmogorov-Smirnov 检验。

关于 Kolmogorov-Smirnov 检验命名的说明

最初发布的 Kolmogorov-Smirnov 方法假定您知道总体的平均值和 SD 值（可能来自以前的工作）。在分析数据时，您很少知道总体的均值和标差。您只知道样本的均值和 SD。因此，Prism 使用 Dallal 和 Wilkinson 近似 P 值的 Lilliefors 方法 (3)。这有时被称为 "Lilliefors 检验"。由于该方法只对较小的 P 值准确，Prism 只对较大的 P 值报告 "P>0.10"。如果您遇到任何差异，您应该知道我们多年前在 Prism 4.01 和 4.0b 中修复了这个检验的一个错误。

我该怎么办？

应该使用哪种测试？一个可能的答案是不使用任何测试。正态性检验远没有许多科学家认为的那么有用。另一个答案是进行所有的检验，并通过观察所有结果得出结论。如果一定要选择一种正态性检验，我们建议使用 D'Ágostino-Pearson 检验，但这是一种非常 "软性 "的建议。如上文所示，在某些情况下，该检验根本无法将某个分布确定为非正态性分布（而它显然不是正态分布）。

 

参考文献                                                                                        

1.P Royston, Remark AS R94：A Remark on Algorithm AS 181：正态性 W 检验》。 英国皇家统计学会杂志。44, No. 4 (1995), pp.

2.RB D'Agostino，"Tests for Normal Distribution" inGoodness-Of-Fit Techniquesedited by RB D'Agostino and MA Stephens，Macel Dekker，1986。

3.Dallal GE and Wilkinson L (1986)，"An Analytic Approximation to the Distribution of Lilliefors's Test Statistic for Normality"，The American Statistician，40，294-296。