示例数据集

为了创建下面的本示例，我输入的数据有两行三列，每个单元格有三个并列重复。没有缺失值，因此总共输入了 18 个值。

我对数据进行了四种分析：假定无重复测量、假定有匹配值堆叠的重复测量、假定有匹配值分布在一行的重复测量以及有双向重复测量。下表用颜色代码解释了这些设计。表格中的每种颜色代表一个受试者。表与表之间的颜色是重复的，但这并不意味着什么。

方差分析表

下表列出了四项分析的方差分析表。以下数值均由 Prism 报告。我对其进行了重新排列和重新命名，以便在一张表中显示这四项分析。

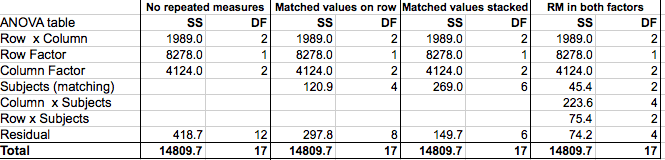
首先关注没有重复测量的平方和 (SS) 列：

•第一行显示行和列的交互作用。它量化了由于行与列之间的差异对所有列来说都不相同而造成的差异程度。同样，它也量化了列间差异对两行而言不尽相同这一事实所导致的变异程度。

•第二行显示的是由于两行之间的系统性差异造成的变化量。

•第三行显示的是列之间的系统差异造成的变化量。

•第二行到最后一行显示的是其他行无法解释的变化。这称为残差或误差。

•最后一行显示所有 18 个值之间的总变异量。

现在看看对相同数据分析的 SS 栏，但对重复测量有不同的假设。

•总 SS 保持不变。这是有道理的。这衡量的是 18 个值之间的总变异。

•交互作用以及行和列的系统效应（前三行）的 SS 值在所有四项分析中都是一样的。

•假设重复测量时，残差的 SS 值较小，因为其中一些变异可归因于受试者之间的变异。在最后一列中，部分变异也可归因于受试者与行或列之间的交互作用。

现在看看 DF 值。

•总 DF 值（最下面一行）为 17。这是数值总数（18）减去 1。无论是否有重复测量的假设，它都是一样的。

•交互作用的 df 等于（列数 - 1）（行数 - 1），因此本示例的 df 为 2*1=2。无论重复测量与否，df 都是相同的。

•行间系统差异的 df 等于行数-1，在本示例中为 1。这与重复测量的结果相同。

•列间系统差异的 df 等于列数-1，本示例中为 2。无论重复测量与否，df 都是相同的。

•受试者的 df 是受试者数减去处理数。当匹配值堆叠在一起时，有 9 个受试者和 3 个处理，因此 df 等于 6。当匹配值在同一行时，有 6 个受试者以两种方式接受治疗（每行一个），所以 df 为 4。当两个因素都有重复测量时，这个值等于受试者人数（3）减去 1，所以 df=2。

有关如何计算 SS 和 DF 的详细信息，请参见 Maxwell 和 Delaney (1)。第 576 页的表 12.2 解释了两个因子的重复测量方差分析表。但请注意，他们使用的术语是 "A x B x S"，而 Prism 使用的是 "残差"。第 595 页的表 12.16 解释了单因素重复测量的双向方差分析表。他们在 Prism 说 "残差"的地方说 "B x S/A"，在 Prism 说 "受试者 "的地方说 "S/A"。

均方值

每个均方值的计算方法都是用平方和值除以相应的自由度。换句话说，对于方差分析表中的每一行，用 SS 值除以 df 值即可计算出 MS 值。

F 比率

每个 F 比值都是通过 MS 值除以另一个 MS 值计算得出的。分母的 MS 值依赖于实验设计。

对于无重复测量的双向方差分析：分母 MS 值总是 MSresidual。

对于单因素中有重复测量方差分析的双向方差分析（Maxwell 和 Delaney 第 596 页）：

•对于交互作用，分母 MS 为 MSresidual

•对于非重复测量因子，分母 MS 为 MSsubjects

•对于重复测量的因子，分母 MS 为 MSresidual

对于双向方差分析，两个因素均为重复测量（Maxwell 和 Delaney 第 577 页）：分母 MS 为被试因素与受试者交互作用的 MS。

•对于行因素，分母 MS 是行因素 x 受试者交互作用的 MS

•对于列因子，分母 MS 是列因子 X 列受试者的交互作用的 MS

•对于交互作用：行因素 x 列因素，分母 MS 为残差（也称为行 x 列 x 受试者的交互作用）

P 值

每个 F 比值都是作为两个 MS 值的比值计算的。其中每个 MS 值都有相应的自由度数。因此，F 比值与分子的一个自由度数和分母的另一个自由度数相关联。Prism 报告如下F (1, 4) = 273.9

根据 F 和两个自由度计算 P 值，可以使用免费的网络计算器或 =FDIST(F, dfn, dfd) Excel 公式来完成

 

 

1.SE Maxwell 和 HD Delaney.设计实验和分析数据：模型比较视角》，第二版。Routledge, 2003.