回顾 P 值和α的含义

解读单个 P 值很简单。考虑比较两个均值的简单情况。假设零假设为真，P 值就是随机抽样导致样本均值差异（或相关性或关联性......）至少与您的研究观察值一样大的概率。

Alpha 是您事先设定的阈值。如果 P 值小于 Alpha，您就认为比较 "统计学显著"。如果您将 alpha 设为 5%，且零假设为真，则有 5%的几率随机抽取受试者，从而根据样本间观察到的差异错误地推断出人群中存在治疗效果。

多重比较

许多科学研究都会测试多个假设。有些研究会产生数百甚至数千次比较。

解读多重 P 值很困难。如果您检验多个独立的零假设，并将每次比较的临界值设为 0.05，那么获得至少一个 "统计学显著"结果的几率大于 5%（即使所有零假设都成立）。这张图说明了问题所在。根据 X 轴上的比较次数（N），用以下公式计算出至少有一个 "显著"比较结果的概率：100(1.00 - 0.95N).

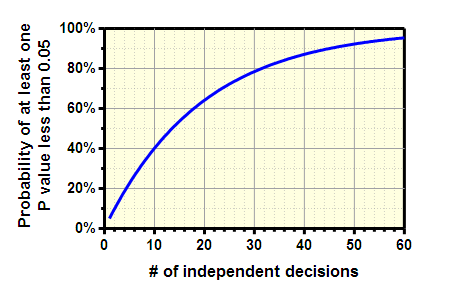
记住不吉利的数字 13。如果您进行了 13 次独立比较，那么偶然获得至少一个 "显著"P 值（<0.05）的几率约为 50%。

上图（以及生成上图的等式）假定比较是独立的。换句话说，它假定任何一个比较出现较小 P 值的概率与任何其他比较出现较小 P 值的概率无关。如果比较不是独立的，就真的无法计算图中所示的概率。

 

示例

我们来看一个示例。您比较了对照组和治疗组动物，并测量了血浆中三种不同酶的水平。您分别对每种酶进行了三次 t 检验，并使用传统的 alpha=0.05 临界值来判定每个 P 值是否显著。即使治疗实际上没有任何作用，您的一个或多个 t 检验也有 14% 的几率 "统计学显著"。

如果您用 10 次 t 检验来比较 10 种不同的酶水平，那么即使治疗真的没有任何作用，仅凭偶然机会获得至少一个 "显著"P 值的几率为 40%。最后，想象一下，您在 10 个时间点测试了 100 种不同的酶，并进行了 12 次前处理......如果你不对多重比较进行校正，你几乎肯定会发现其中一些是 "显著的"，即使真的所有零假设都是真的。

您只能对您知道的比较进行校正

在阅读研究报告时，只有当您了解研究者所做的所有比较时，才能对多重比较进行解释。如果他们只报告 "显著 "差异，而不报告比较的总数，就无法正确评估结果。理想情况下，所有分析都应在收集数据前进行规划，并报告所有分析结果。

了解更多

多重比较是一个大问题，几乎影响所有统计结果的解读。更多信息，请参阅下文摘录的贝里的评论(1)，或《直观生物统计学》(2) 第 22 章和第 23 章。

"大多数科学家对多重性问题熟视无睹。然而，它们无处不在。多重性以一种或多种形式存在于每一种统计应用中。它们可能是公开的，也可能是隐藏的。即使它们是公开的，认识它们也不过是艰难推论过程的第一步。乘数问题是我们统计学家面临的最棘手的问题。它们威胁着每一个统计结论的有效性"(1)

1.Berry, D. A. (2007).难以解决且无处不在的多重性问题。医药统计学》，6，155-160 页

2.Motulsky, H.J. (2010).直观生物统计学》，第 3 版。牛津大学出版社。ISBN=978-0-19-994664-8.