线性回归的工作原理是拟合一个模型，在给定 X 值的情况下，您可以用这个模型来确定 Y 的实际值。这个模型提供了这两个变量之间关系的信息，并回答了这样一个问题：Y 的值随 X 的变化而变化多少？换句话说，使用线性回归模型，如果能很好地定义数据，那么只需知道预测因子的值，就能合理地预测结果的值。相比之下，逻辑回归模型则是在给定预测因子值的情况下，观察到成功的概率。以下面显示的数据为例：

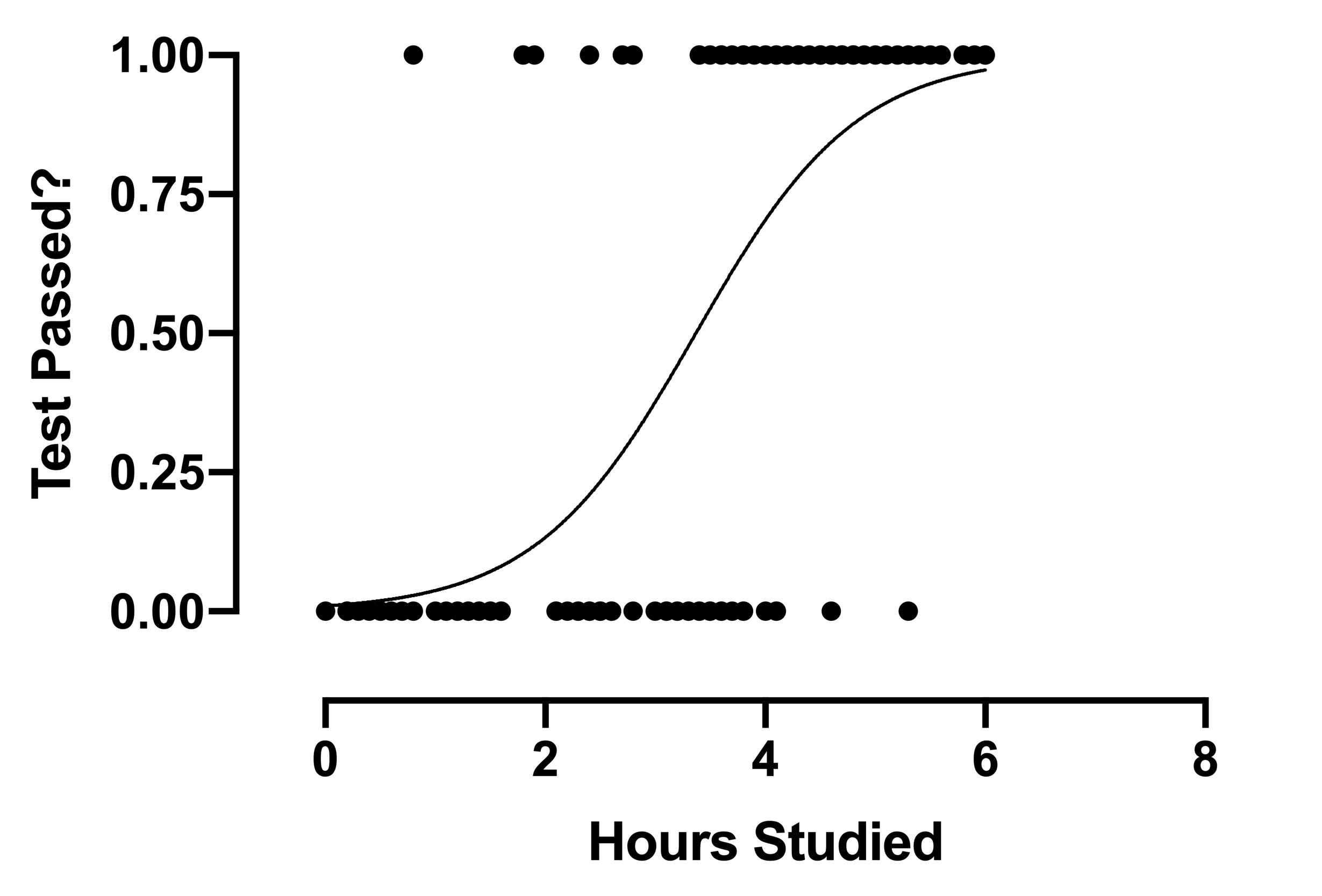
在这幅图中，所有数据点的值要么是 0（失败），要么是 1（通过）。逻辑拟合是 S 曲线，它将成功概率作为学习时数的函数进行建模。在本示例中，教师会很高兴地发现，学习 4 小时的学生很少有考试不及格的。事实上，对于学习 4 小时的学生来说，模型预测的通过概率约为 70%。

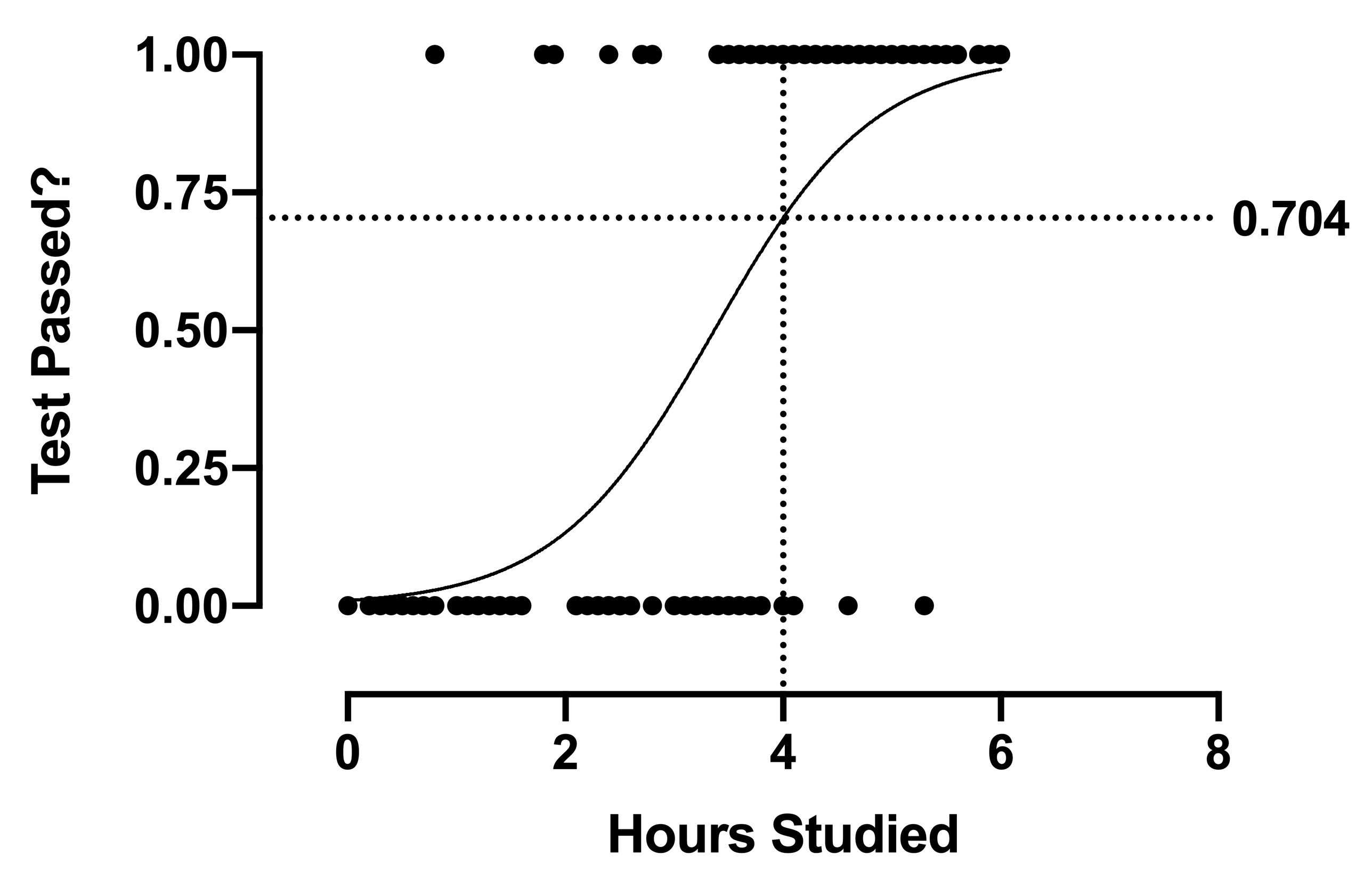
S 曲线是逻辑函数估算概率的副产品。请注意，概率的边界在 0 和 1 之间，这是有道理的：不可能有 "负概率 "的事件发生，而大于 100%的概率也没有任何意义。因此，S 曲线的上限和下限也受到这些值的限制。但这意味着--与线性回归不同--我们从模型中得到的值并不能直接估算出我们期望观察到的值。当 X = 4 时，模型值为 0.704。然而，对于我们在 X = 4 处进行的任何观察，结果都只会是 0 或 1；观察值永远不会是 0.704。模型只是告诉我们，在 X = 4 时，我们可以预期 ~70% 的结果是 1。这是逻辑回归的一个关键点。

如果我们在相同的数据上比较逻辑回归模型和线性回归模型，我们很快就会明白为什么简单的线性回归模型对这类数据根本不起作用。

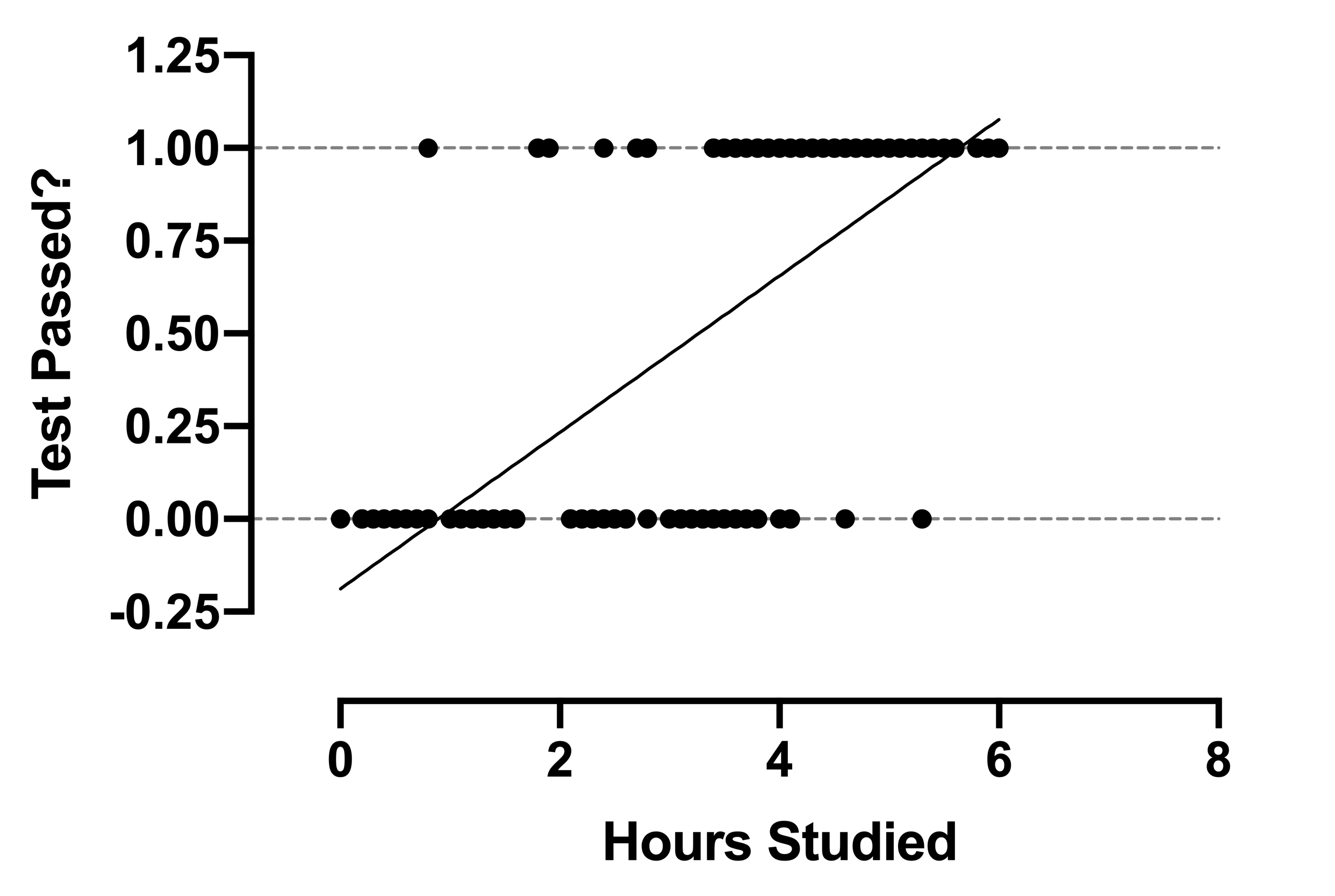
我们的数据仍然是 0 和 1，但与逻辑模型不同的是，线性模型预测的不是成功的概率。相反，它预测的值可以小于 0，也可以大于 1。例如，本示例预测学习时间少于约 0.9 小时的学生通过检验的估计值为阴性。在某些情况下，线性模型可用于二元自变量，进行简单分类。但是，这些方法无法提供系数的可解读性、显著性检验和置信区间。对于这些结果（当您的结果是二元时），请使用逻辑回归。