如何绘制二项分布或泊松分布图

下载 Prism 文件。

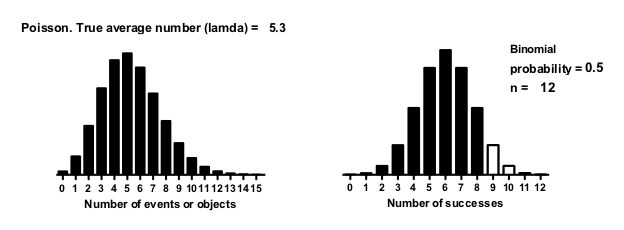
要修改该文件，请更改信息表中的 lamda 值（泊松分布）或概率、n 和截止值（二项分布）。输入新值后，图形就会更新。本示例很好地说明了将信息常量与分析挂钩的实用性。

如果您想重新创建类似的图表，请记住以下几点：

•顾名思义，"创建理论曲线族 "分析通常用于创建曲线，而不是条形图。选择 X 值范围时，指定适当数量的 "线段"（点），以便 X 间隔等于 1.0。左边的二项式本示例创建了 16 个 "线段"，从 X=0 开始，到 X=15 结束。右边的泊松例子创建了 13 个 "线段"，X 从 0 开始，到 13 结束。

•分析将创建一组线段（试图创建一条曲线）。单击 "更改图形类型"按钮，或下拉 "更改"菜单并选择 "图形类型"。然后选择分组选项卡，再选择交错条形图。

•右边的二项式本示例有两个数据集。你不希望按照上一步的选择将它们交错绘制。双击调出设置图表格式，然后转到中间选项卡，选择将第二个数据集叠加到第一个数据集上（而不是交错）。并为其指定不同的颜色。

数学细节

二项分布

当每次试验的成功概率为 P 时，N 次试验中正好有 X 次成功的概率方程为

R=INT(X+0.5)

精确概率=（P^R）*（1-P）^（N-R）；N 次试验中成功的精确概率

NRearrangments=exp(gammaln(N+1) - gammaln(R+1) - gammaln(N - R +1)) 

gamma(J)=(J-1)阶乘，或 (J-1)！但阶乘在 Prism 中不是一个函数

;NRearrangments=N!/(R！(N-R)! 

H=ExactProb * NRearrangments

<A>Y=H

<B>Y=IF(X>cutoff, H, 0)

 

 

泊松分布

泊松分布的公式是

Y=exp(-1*Lamda)*Lamda^X/gamma(X+1)

注意伽马函数的定义

gamma(i) = factor(i-1) 

gamma(x+1)= factor(x) = X！