什么是线性-二次模型？

哺乳动物细胞在受到剂量为 D 的辐射照射后死亡，通常遵循线性-二次模型 (1-3)。

存活细胞数 = e-(A*D + B*D^2)

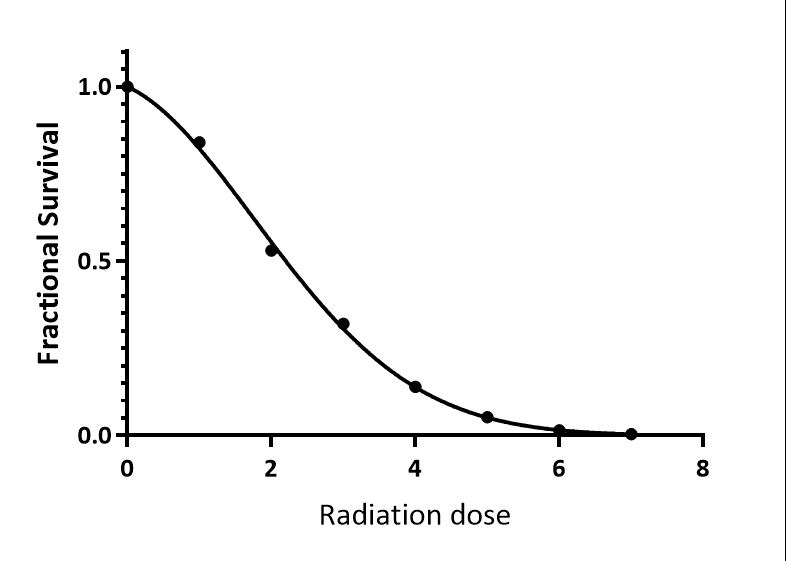
线性-二次模型由 Chadwick 和 Leenhouts (2) 提出。他们提出，线性分量（A*X）代表由于 DNA 受到一次致命撞击而导致的细胞死亡，二次分量（B*X2）代表只有受到两次撞击才会导致的细胞死亡。 然而，现在很明显这种机制并不正确，LQ 参数 A 和 B 的生物学解读也不清楚（3）。

尽管我们不知道该模型的生物学基础，但它对辐射诱导的细胞死亡进行了合理的描述，也许在辐射剂量非常高的情况下除外。Bodgi 等人回顾了线性-二次方程和一些替代方案（3），并提出了一个与线性-二次模型相对应的生物学模型（4）。

有时 Y 轴被绘制成分数存活率的对数轴，而不是分数存活率本身。

参考文献

Brenner, D. J. (2008).线性-二次模型是确定每分数大剂量等效剂量的适当方法，18/4: 234-9。Elsevier.

Chadwick, K.H., Leenhouts, H.P., 1973.细胞存活的分子理论。Phys.13, 78-87.

Bodgi, L., Canet, A., Pujo-Menjouet, L., Lesne, A., Victor, J.-M., & Foray, N. (2016).辐射作用于活细胞的数学模型：从目标理论到现代方法。历史与评论。理论生物学杂志》，394：93-101。DOI: 10.1016/j.jtbi.2016.01.018

Bodgi, L., & Foray, N. (2016).以 ATM 蛋白的核关闭为基础的辐射响应新理论：线性-二次模型的解析。国际辐射生物学杂志》，92/3: 117-31.DOI: 10.3109/09553002.2016.1135260