什么是分段回归？

在某些情况下，您可能希望对数据的不同部分拟合不同的模型。这就是所谓的分段回归。这通常发生在动力学实验中，即在记录数据的同时添加药物或进行某种干预。干预前收集的值与干预后收集的值遵循不同的模型。

如果您没有在 X 轴上的特定时间进行干预，那么这种分段回归就不太可能是分析的首选。

如何使用 Prism 进行分段回归

虽然 Prism 没有内置方程来拟合不同部分的数据，但您可以使用包含 IF 函数的用户自定义方程来达到这种效果。

在本示例中，您收集的数据在实验早期建立了基线，直到 "开始"。然后，您添加了一种药物，并跟踪结果（Y）向高点增加的过程。在注射之前，数据沿着一条水平线；注射之后，数据形成了一条指数关联曲线。

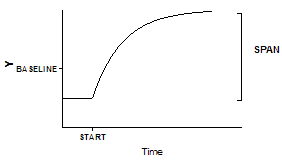
Y1=基准线

Y2=BASELINE + SPAN*(1-exp(-K*(X-START)))
Y=IF[(X<START),Y1,Y2)]

 

首先阅读最下面一行，最容易理解这个等式。当 X 值小于 START 时，Y 等于 Y1，即基线。否则，Y 等于 Y2，这是由指数关联方程定义的。

该方程有两个中间变量（Y1 和 Y2）。Prism 可以拟合四个真实变量：START、SPAN、K 和 BASELINE。

在很多情况下，您会将 START 设为常数，等于实验干预的时间。如果您希望 Prism 拟合 START，请谨慎选择初始值。

这种模型最适合 X 为时间的情况，在特定时间点发生的事情会改变模型。在上面的本示例中，在 time=Start 时注射了一种药物。

如何仅对部分数据拟合模型

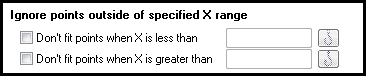
非线性回归对话框的 "范围"选项卡可让您定义一个 X 范围，以确定哪些点被拟合，哪些点被忽略。