什么是残差？

非加权拟合

残差是一个点与曲线的距离。最小二乘回归的目的是最小化这些残差的平方和。 当点在曲线上方时，残差为正，当点在曲线下方时，残差为负。绘制残差图，查看数据与所选模型的吻合程度。数据与模型的轻微偏差往往比数据与曲线的残差图更容易发现。

加权拟合

如果您选择对数据进行不等权重，Prism 会相应调整残差的定义。

Prism 制表并绘制的残差图等于前段定义的残差除以加权因子。 最常见的通用替代权重是 "按1/Y2加权（最小化相对距离平方）"。在这种情况下，残差被定义为点到曲线的距离除以曲线的 Y 值。加权非线性回归最小化这些残差的平方和。请注意加权定义的模糊性。Prism 对话框提供了按1/Y2 加权的选择。这意味着残差平方除以Y2。加权非线性回归最小化这些加权残差的平方和。

早期版本的 Prism（直到 Prism 4）总是绘制基本的非加权残差图，即使您选择对点进行不等量加权。

哪种残差图？

Prism 提供了五种类型的图形，可用于研究模型拟合的残差：

Prism 允许您创建任意数量的非线性回归残差图。只需选择要与分析结果一起包含的残差图名称旁边的复选框即可。

本示例

拟合本示例

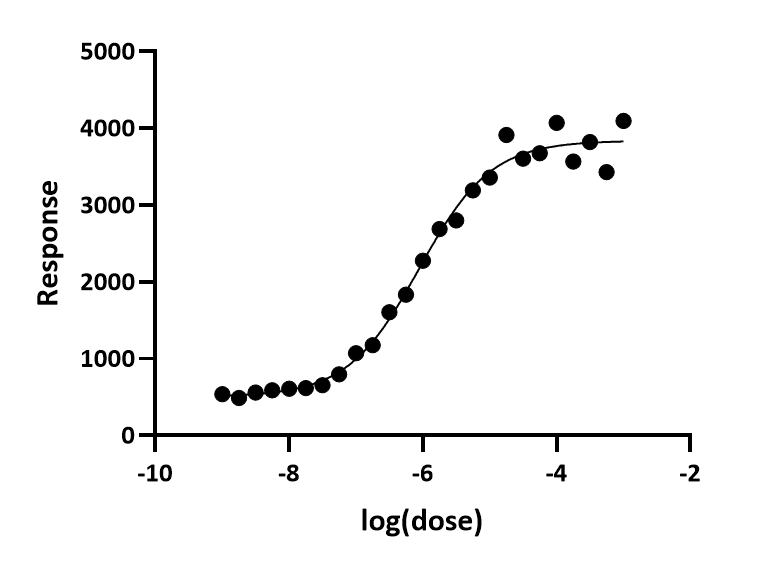
下面是使用模拟数据绘制的对数（剂量）与反应曲线。随机散点的选择是为了让 Y 值较大的点具有较大的平均散点。拟合采用常规方法，没有加权。如果仔细观察，可以发现曲线顶部的点散度较大，但并不明显。

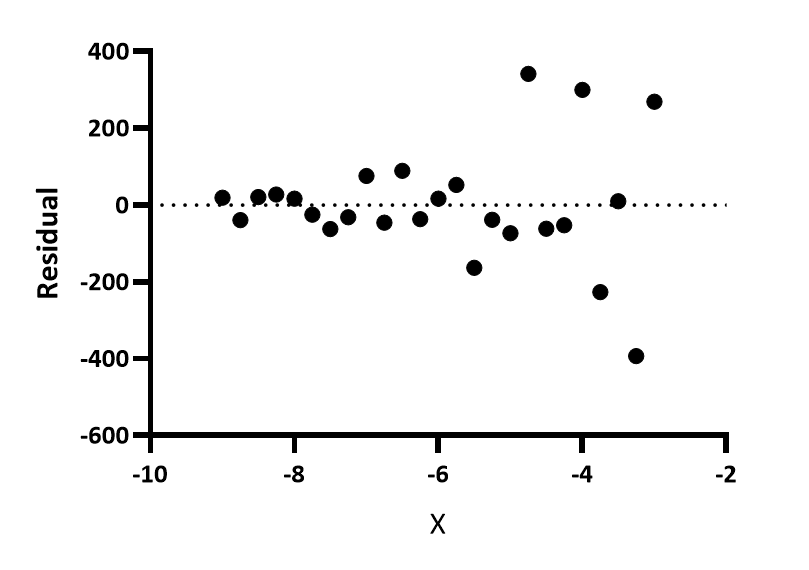
残差与 X

这是最常见的残差图。Prism 7 及更早版本只创建了这种残差图。可以看出，X 值大的点的残差（正值和负值）也较大。

 

残差与预测 Y

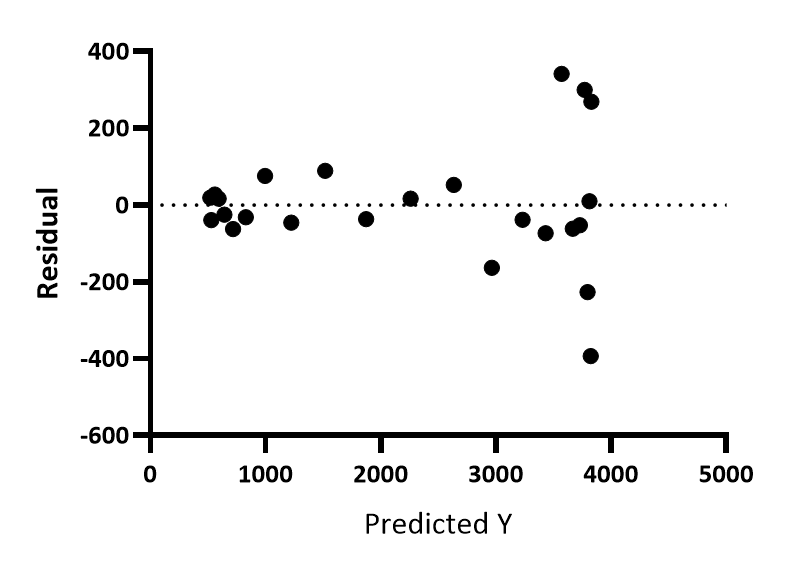
对于每个点，Prism 都会计算该 X 值处的曲线 Y 值，并将该 Y 值绘制在残差图的 X 轴上。残差图的 Y 轴绘制的是残差或加权残差图。可以看出，Y 值越大的点，残差也越大，正负都是如此。

在本示例中，Y 值随着 X 值的增大而增大。所以这张图看起来和残差与 X 的关系图没有太大区别。但如果曲线是双相的，这两个图看起来就会有更大的不同。

同方差性图

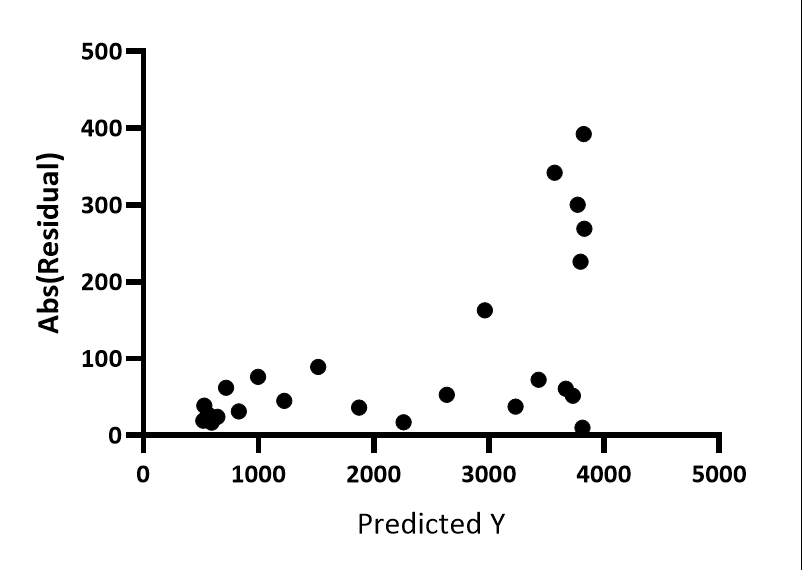
这张图的制作和预测 Y 与残差的关系图一样，只不过这里显示的是残差的绝对值。现在可以清楚地看到，Y 越大，残差越大。

QQ 图

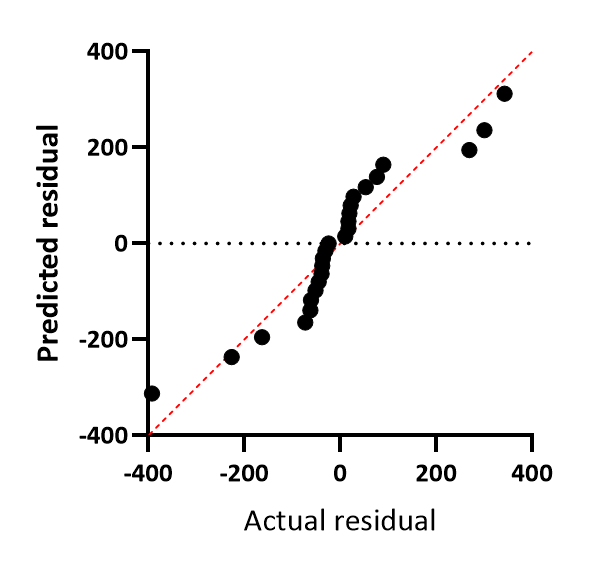
X 轴绘制实际残差图或加权残差图。Y 轴绘制的是假设从高斯分布中采样的预测残差图（或加权残差图）。回归的一个假设是残差是从高斯分布中采样的，通过该图可以评估这一假设。如果假设成立，则所有点都应非常接近图中红色显示的特征线。QQ 图有时会将一个或两个坐标轴绘制成百分位数或量化数（与百分位数相同，但为分数而非百分比）。Prism 始终将两个坐标轴绘制成与数据 Y 值相同的单位。

在本示例中，数据并没有很好地遵循同一直线。数据是从高斯分布中采样的，但当 Y 值较大时，该分布的 SD 值较大。残差并非从单一的高斯分布中采样，这也是各点与同一直线之间存在系统差异的原因。

实际与预测图

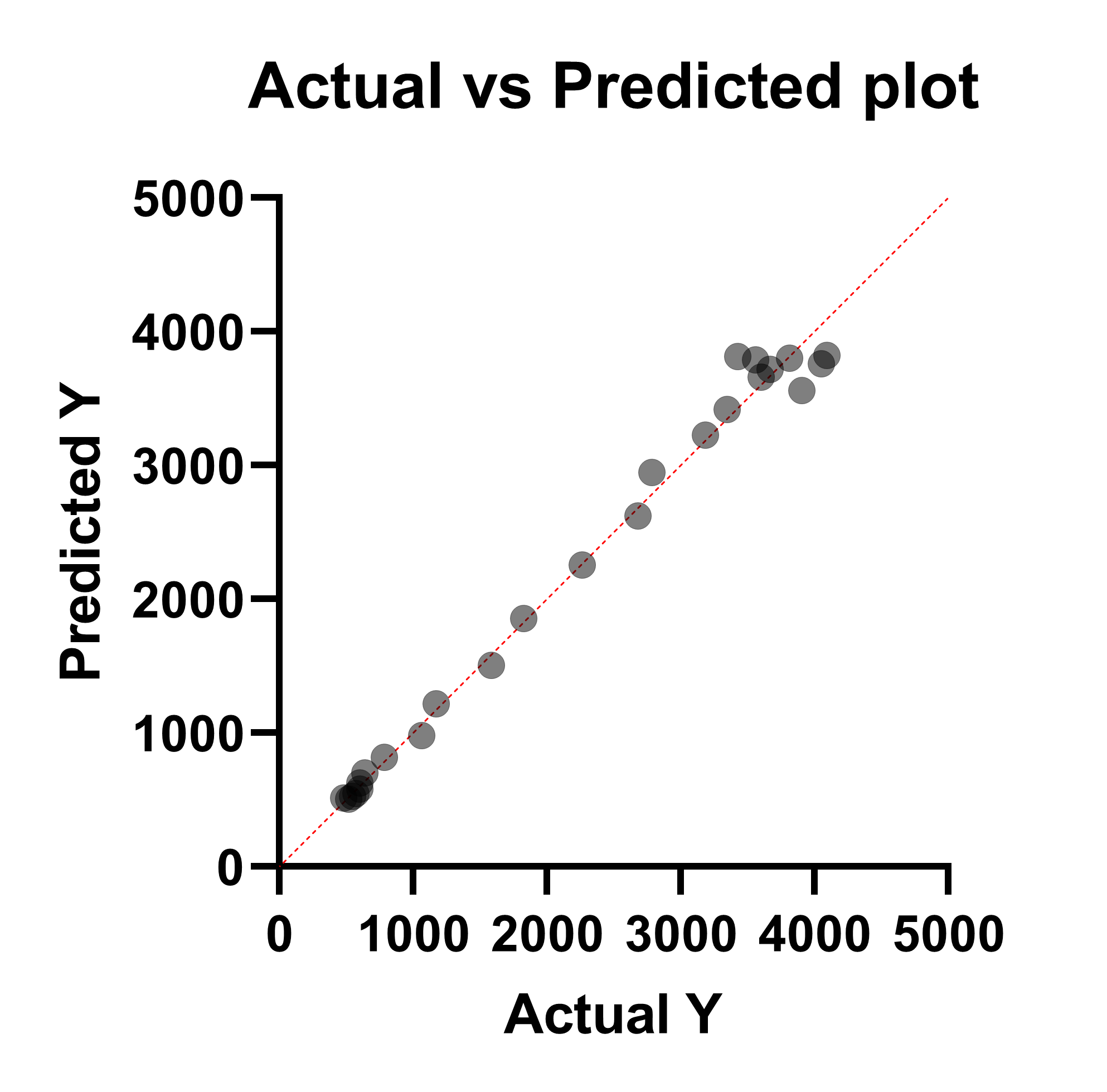
这张图没有直接将拟合的残差图绘制在任一坐标轴上。相反，此图将实际 Y 值（在数据表中输入）绘制在 X 轴上，将预测 Y 值绘制在 Y 轴上。此图通常用于评估简单线性回归的拟合（Prism 也会为多元线性回归生成此图），但不常用于非线性 回归。在这种情况下，残差用所绘制点与红色标识线之间的垂直距离来表示（也可以使用水平距离，因为这些距离对于每个点来说总是相同的）。

虽然在非线性回归中使用这种图形不是标准的，但这种图形仍然可以作为一种手段来研究模型对测量结果（依赖度）变量的预测效果如何。从上图可以看出，当 Y 值较低时，模型对实际值的预测效果较好（点更接近同一直线），而当 Y 值较高时，预测结果与实际值相差较远（点更远离同一直线）。

但必须注意的是，仅仅因为模型能很好地预测数据（换句话说，曲线经过的每一点都非常接近），并不表明模型是正确的！在非线性回归中，只要有足够多的项，就可以生成一条几乎完美通过每个点的任意曲线。在尝试解读这幅图之前，请确保您使用的模型在科学上是合理的。

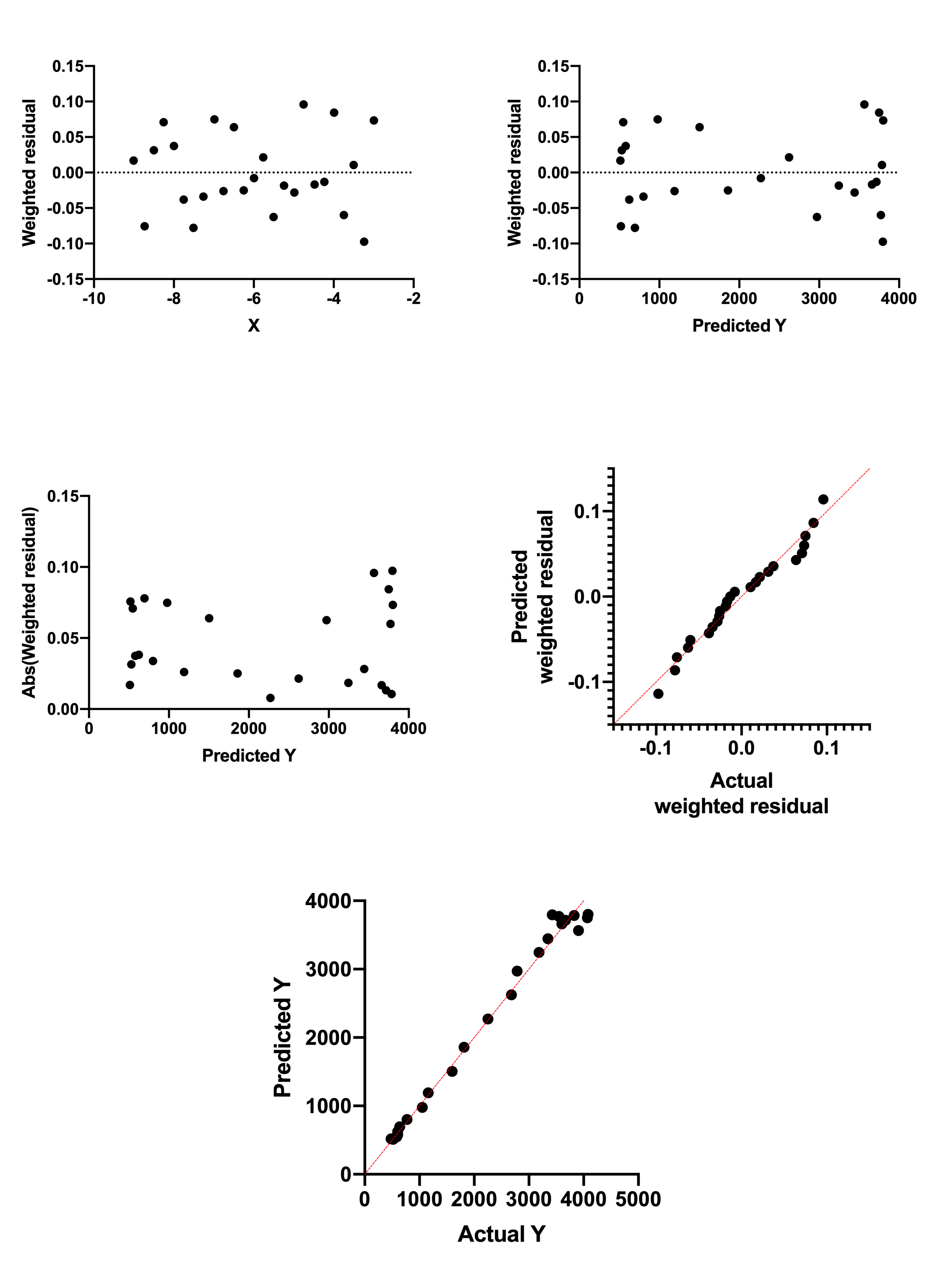
用加权回归拟合的同一本示例

然后将数据拟合到相同的模型中，但采用了相对权重。以下是五a残差图。所有数据都显示现在符合拟合假设。